Leonardo Bigollo (Leonardo Pisano o de Pisa) fue un matemático que vivió en Italia entre los siglos 12 y 13 (1170-1240) y que se atrevió a despreciar el sistema de números romanos que imperaba en su época. Ha pasado a la historia con el que fuera su apodo: Fibonacci, un derivado de la suma de los vocablos fillius + bonnacci que en latín e italiano significan algo así como “hijo del bien intencionado”. Al parecer, el padre de Fibonacci (Guglielmo) era buena gente, además de dedicarse al comercio viajando por el norte de África. Fue allí donde su hijo Leonardo descubrió la magia de los números árabes.

Retrato de Fibonacci / Imagen: wikimedia

El sistema indoarábigo viajó desde la India primero a Persia y después a Oriente Medio y el norte de África, desde donde dio el salto a Europa, gracias, entre otros matemáticos, a Fibonacci. El uso de los números árabes que planteaba el pisano incluía la posibilidad de operar con números enteros y fracciones, la división de un número en factores primos, la operación de la raíz cuadrada… No fue fácil adoptar este sistema a pesar de sus numerosas ventajas. Las cruzadas contra el Islam que estaban en marcha por aquel entonces, hacía que cualquier cosa etiquetada como “árabe” quedara automáticamente bajo sospecha. Los números árabes llegaron incluso a ser vetados en la ciudad de Florencia en 1299 con el pretexto de que “eran más fáciles de falsificar que los números romanos”.

Gracias a la actividad comercial de su padre, Fibonacci tuvo la oportunidad de conocer a los grandes matemáticos que había fuera de la burbuja de occidente (Egipto, Siria, Argelia, Grecia…) durante largos viajes a través de diferentes países del mundo árabe y del Mediterráneo. Después regresó a Italia y cuando tenía 32 años publicó el libro Liber abaci (1202), en el que explicaba la importancia del sistema de numeración árabe y lo aplicaba a diferentes situaciones del día a día del mundo del comercio para probar que era más práctico que el sistema de números romanos: el cambio de divisas, la contabilidad comercial, la transformación de pesos y medidas… Un cuarto de siglo más tarde (1227) publicó una segunda edición del mismo libro ampliada y reelaborada que se ha convertido en la versión de referencia de “Liber abaci”, pues actualmente no se conserva ninguno de los ejemplares de aquella primera edición manuscrita de 1202.

Federico II de Hohenstaufen (1194-1250) era el Emperador del Sacro Imperio Romano Germánico cuando conoció el trabajo de Fibonacci gracias a la correspondencia que mantuvo el matemático tras su vuelta a Italia con algunos miembros de su corte, entre los que se encontraba Michael Scotus, astrólogo a quien admiraba el pisano y al que dedicó esa segunda edición de su libro más famoso. Johanes de Palermo(Juan de Palermo) también formaba parte de la Corte y fue él quien retó a Fibonacci con un problema matemático que grabaría su nombre en la historia para siempre.

EL PROBLEMA DE LOS CONEJOS

Un hombre puso un par de conejos en un lugar rodeado por todos lados por una pared. ¿Cuántos pares de conejos pueden ser producidos a partir de ese par en un año si se supone que cada mes, cada pareja engendra un nuevo par que a partir del segundo mes se vuelve productivo?

Un hombre puso un par de conejos en un lugar rodeado por todos lados por una pared. ¿Cuántos pares de conejos pueden ser producidos a partir de ese par en un año si se supone que cada mes, cada pareja engendra un nuevo par que a partir del segundo mes se vuelve productivo?

Fibonacci aceptó el reto y resolvió el problema, publicando la solución en una obra titulada “Flos” (1225). Para ello desarrolló una serie numérica que pasaría a la historia como la serie de Fibonacci.Dicha sucesión de números comienza con 0 y 1, y a partir de ahí cada elemento o número de Fibonacci es la suma de los dos anteriores. Así representó Leonardo el problema reproductivo de los conejos que, aunque es un modelo artificial en el caso de estos animales (pues biológicamente no es estrictamente cierto) sí se cumple a la perfección en el modelo reproductivo de las abejas. En una colmena, sólo se reproduce la reina: es la única que pone huevos.

• Si son fertilizados, surgen las abejas obreras (hembras). Con un 50 % de su carga genética aportada por la madre (reina) y el otro 50 por el padre (zángano).
• Los zánganos o abejas macho se producen a partir de huevos no fertilizados. Así, las abejas obreras hembras tienen dos progenitores y los
• zánganos, uno. El 100% de su información genética es aportada por la madre.

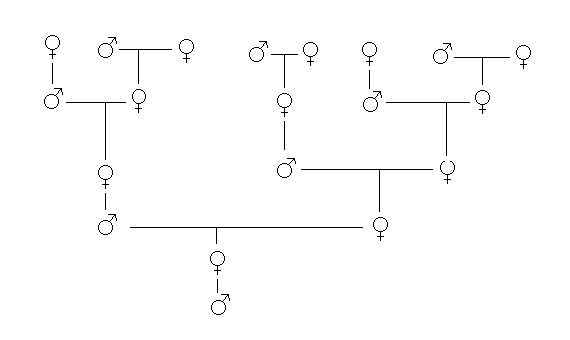
Esquema simulando el árbol genealógico de las abejas / Imagen:Canada’s SchoolNet

Las abejas no son una excepción, pues estos números están detrás de muchos y muy variopintos fenómenos de la naturaleza: la disposición de los pétalos de las flores, la formación de los huracanes… ¿Cómo es posible? ¿Acaso son una combinación mágica, el “abracadabra” de las matemáticas? El misterio detrás de esta sucesión de números que parece estar inscrita en los cimientos matemáticos de todo lo que nos rodea (al menos de muchas de las cosas que existen a nuestro alrededor) fascina a expertos de muchos campos de la ciencia desde hace siglos, llegando incluso a existir publicaciones especializadas en encontrar nuevos campos relacionados con ella.

DE LAS MATEMÁTICAS MEDIEVALES A LA “DIVINA PROPORCIÓN”

Pero, ¿cuánto hay de “magia” en la famosa serie de Fibonacci? ¿Hasta qué punto fue el pisano el descubridor exclusivo de estos números y las proporciones a las que da lugar la relación entre los mismos? La historia ha dejado pistas sobre anteriores menciones de la fórmula, como es el caso de varios matemáticos hindúes: Gopala (1135) y Hemachandra (1150), que ya habían dado cuenta de ella en sus escritos varias décadas antes de la existencia de Fibonacci. Incluso varios siglos después, el mismísimo Kepler (1571-1630) continuó fascinado con la investigación sobre esta serie y desarrolló siglos después el concepto que pasaría a la historia como “la divina proporción”  en su obra “Strena Seu de Nive Sexangula” (1611).

Kepler redescubrió la secuencia a través de la proporción que existía entre los términos consecutivos de la serie.  2 es a 3, lo que 3 es a 5 y lo que 5 es a 8 y así sucesivamente con todos los elementos de la misma. Es decir, existe una proporción (divina proporción o proporción áurea) que se mantiene constantemente al dividir cualquiera de los números entre su predecesor en la serie. Esta proporción se representa con el número phi (en honor al escultor griego Fidias y no a Fibonacci): φ = 1,618.

Kepler ya definió en su obra “Strena Seu de Nive Sexangula” (1611) la importancia de esta proporción, que según él, se desarrollaba de una manera análoga en el proceso reproductivo, consiguiendo así perpetuarse. La idea de Kepler sobre un proceso biológico de autorreplicación marcado por la secuencia de Fibonacci fue ignorada por los biólogos hasta hace relativamente poco, cuando la filotaxis  -disposición de las hojas en un tallo- se consolidó científicamente.

Sea como fuere, el descubrimiento de la serie numérica que dio lugar a la divina proporción le valió a Fibonacci la permanencia en el tiempo y en la memoria de las matemáticas. En el siglo XIX una estatua en su honor fue erigida en Pisa y a día de hoy puede visitarse en el cementerio de la ciudad, en la Piazza dei Miracoli. No hay muchos datos sobre el final de su vida, aunque sí existe un decreto por el cual la República de Pisa concede un salario vitalicio a Leonardo pisano en 1240 en reconocimiento por su servicio a la ciudad como consejero en materias de contabilidad.

Dory Gascueña